分类
Level6

二叉树

一、二叉树的概念
二叉树 的每个结点至多只有二棵子树(不存在度大于2的结点)。二叉树的子树有左子树、右子树。其次序不能颠倒。所以二叉树是一棵严格的有序树。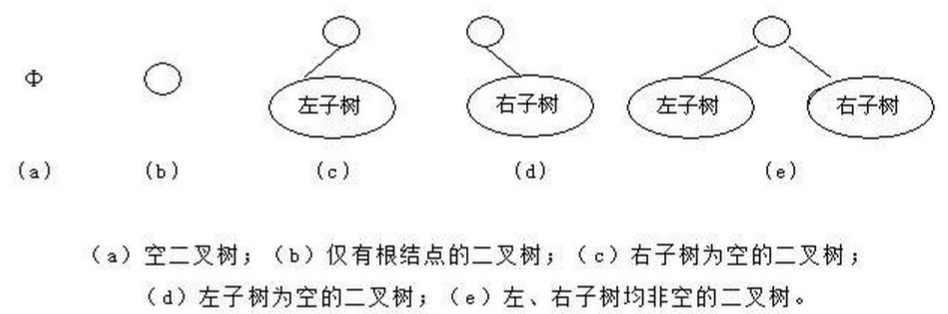
练习：按照二叉树的定义，4个节点的二叉树有多少种？（）
A 13
B 14
C 15
D 16

分析  设n个结点的二叉树有f(n)种，对于f(4), 分类讨论:
左子树有0个结点，右子树有3个结点, 种数为f(0)*f(3)
左子树有1个结点，右子树有2个结点, 种数为f(1)*f(2)
左子树有2个结点，右子树有1个结点, 种数为f(1)*f(2)
左子树有3个结点，右子树有0个结点, 种数为f(1)*f(2)

f(0)=1,f(1)=1,f(2)=2,f(3)=(1,1,2)*(2,1,1)=5
f(4)=f(0)*f(3)+f(1)*f(2)+f(2)*f(1)+f(3)*f(0)
f(4)=(1,1,2,5)*(5,2,1,1)=14

二叉树节点算法 (2n)!/(n!*(n+1)!) 或者\(C_{2*n}^{n}\)/(n+1)

二、二叉树的分类

满二叉树 完美二叉树 (perfect binary tree) 除最后一层无任何子结点外，每一层上的所有结点都有两个子结点。也可以这样理解，除叶子结点外的所有结点均有两个子结点。结点数达到最大值，所有叶子结点必须在同一层上。

满二叉树的性质(设根结点的深度是1):
1、一颗树深度为h，最大层数为k，深度与最大层数相同，k=h;
2、叶子数为2h-1;
3、第k层的结点数是：2k-1
4、总结点数是：2k-1，且总结点数一定是奇数

完全二叉树 (complete binary tree) 若设二叉树的深度为h，除第 h 层外，其它各层 (1～ (h-1) 层) 的结点数都达到最大个数，第h层所有的结点都连续集中在最左边，这就是完全二叉树。
注：完全二叉树是效率很高的数据结构，堆是一种完全二叉树或者近似完全二叉树，所以效率极高，像常用的排序算法、Dijkstra算法、Prim算法等都要用堆才能优化，二叉排序树的效率也要借助平衡性来提高，而平衡性基于完全二叉树。

完全二叉树特性 若对含 n 个结点的完全二叉树从上到下且从左至右进行 1 至 n 的编号，则对完全二叉树中任意一个编号为 i 的结点有如下特性:

  • 若 i = 1，则该结点是二叉树的根，无双亲, 否则，编号为 [i/2] 的结点为其双亲结点;
  • 若 2i > n，则该结点无左孩子，否则，编号为 2i 的结点为其左孩子结点；
  • 若 2i+1 > n，则该结点无右孩子结点， 否则，编号为 2i+1 的结点为其右孩子结点。

完整二叉树 (full/proper binary tree) 每个结点的子结点数量均为 0 或者 2 的二叉树。换言之，每个结点或者是树叶，或者左右子树均非空。

三、二叉树的重要特性

  1. 二叉树的第 k 层上结点数最多为 2k-1；
  2. 高度为 h 的二叉树中，最多有 2h-1 个结点；
  3. 对任何一棵二叉树, 如果叶结点数为n0 , 度为2的结点数为n2 , 则一定满足n0=n2+1。
证明:
1.假设度为 1 的结点个数为 n1，结点总数为 n，B 为二叉树中的分支数。因为在二叉树中，所有结点的度均小于或等于 2，所以结点总数为：n=n0+n1+n2
2.再查看一下分支数。在二叉树中，除根结点之外，每个结点都有一个从上向下的分支指向，所以，总的结点个数 n与分支数 B 之间的关系为：n=B+1。又因为在二叉树中，度为 1 的结点产生 1 个分支，度为 2 的结点产生 2 个分支，所以分支数 B 可以表示为：B=n1+2n2。
3.用上面2个式子得到n0=n2+1。
  1. 二叉树的子树有左、右之分，顺序不能颠倒。
  2. 具有 n 个结点的完全二叉树的深度为 floor(log2n)+1;
  3. 有 n 个结点的完全二叉树各结点如果用顺序方式存储，则结点之间有如下关系：
    • 若i为结点编号则 如果 i>1，则其父结点的编号为 i/2;
    • 如果2i <= n，则其左儿子（即左子树的根结点）的编号为2i；若2i>n，则无左儿子；
    • 如果 2i+1 <= n，则其右儿子的结点编号为 2i+1；若 2i+1>N，则无右儿子。
  1. 给定n个结点，能构成h(n)种不同的二叉树，其中h(n)为卡特兰数的第n项，h(n)=C(2*n, n)/(n+1)。

四、二叉树的存储
二叉树的顺序存储 二叉树的顺序存储结构就是使用一维数组存储二叉树中的结点，并且结点的存储位置，就是数组的下标索引。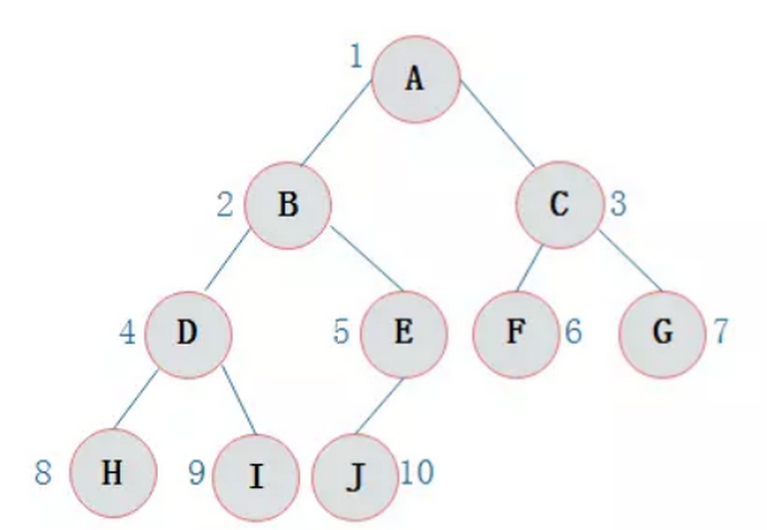二叉树的链式存储：采用链式存储结构的二叉树。二叉树每个结点最多有两个孩子，所以为它设计一个数据域和两个指针域是比较自然的想法。

二叉树的遍历 二叉树的遍历是指从根结点出发，按照某种次序依次访问二叉树中所有结点，使得每个结点被访问一次且仅被访问一次。二叉树的遍历次序不同于线性结构，最多也就是从头至尾、循环、双向等简单的遍历方式。树的结点之间不存在唯一的前驱和后继关系，在访问一个结点后，下一个被访问的结点面临着不同的选择。
前序遍历 规则是若二叉树为空，则返回，否则先访问根结点，然后前序遍历左子树，再前序遍历右子树。遍历顺序为：「根结点–>左孩子–>右孩子」.
中序遍历 规则是若树为空，则空操作返回，否则从根结点开始（注意并不是先访问根结点），中序遍历根结点的左子树，然后是访问根结点，最后中序遍历右子树。遍历顺序为：「左孩子–>根结点–>右孩子」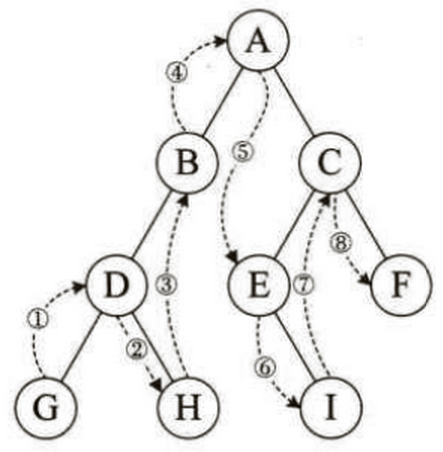
后序遍历 规则是若树为空，则空操作返回，否则从左到右先叶子后结点的方式遍历访问左右子树，最后是访问根结点。遍历顺序为：「左孩子–>右孩子–>根结点」
层序遍历 规则是若树为空，则空操作返回，否则从树的第一层，也就是根结点开始访问，从上而下逐层遍历，在同一层中，按从左到右的顺序对结点逐个访问。
在竞赛中, 经常使用数组来存放二叉树的结点信息, 左右子树的结点可以使用数组下标来代替指针。